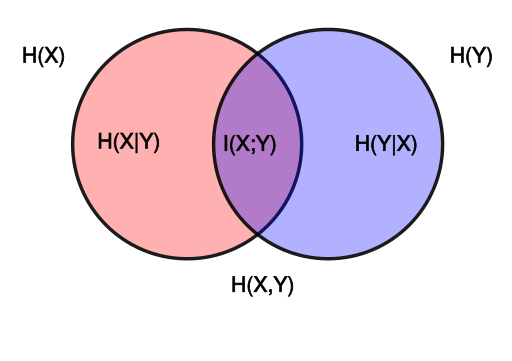
Measuring Entropy Reduction: How much reduction in the entropy of X can we obtain by knowing Y?

$$I(X; Y)= H(X) – H(X|Y) = H(Y)-H(Y|X) = H(X) + H(Y) - H(X,Y)$$

Properties

• symmetric
• non-negative
• I(X;Y)=0 iff X and Y are independent

Formally:

$${\displaystyle I(X;Y)=\int _{Y}\int _{X}p(x,y)\log {\left({\frac {p(x,y)}{p(x)\,p(y)}}\right)}\;dx\,dy}$$

Expressed by KL Divergence:

$$I(X;Y)=D_{\mathrm {KL} }(p(x,y)\|p(x)p(y))$$
MI measures the divergence of the actual joint distribution from the expected distribution under the independence assumption.

Furthermore,

$${\begin{aligned}I(X;Y) &{}=D_{\mathrm {KL} }(p(x,y)\|p(x)p(y))\\ &{}=\int p(x,y)\log\frac{p(x,y)}{p(x)p(y)} \mathrm dx \mathrm dy\\ &{}=\int p(x|y)p(y)\log\frac{p(x|y)}{p(x)} \mathrm dx \mathrm dy\\ &{}=\int p(y)\left(\int p(x|y)\log \frac{p(x|y)}{p(x)}\mathrm dx\right)\mathrm dy\\ &{}=\operatorname {E} _{Y}\{D_{\mathrm {KL} }(p(x|y)\|p(x))\} \end{aligned}}$$
Thus, MI can also be understood as the expectation of the Kullback–Leibler divergence of the univariate distribution p(x) of X from the conditional distribution p(x|y) of X given Y: the more different the distributions p(x|y) and p(x) are on average, the greater the information gain.

Reference

Mutual Information: https://en.wikipedia.org/wiki/Mutual_information
Text Mining: https://www.coursera.org/learn/text-mining